Если вы думаете, что у вашего ребенка нет способностей к математике, то это ошибка. Профессор Стэнфорда Джо Боулер утверждает: все ограничения — в голове, а научиться мыслить математически можно в любом возрасте. В книге «Безграничный разум» она показывает, какие типы заданий помогают настроить свой мозг на новое мышление, творческое и без ограничений. Смысл некоторых техник не в том, чтобы в точности повторить эти задания. Гораздо полезнее будет применять сам принцип во время выполнения домашней работы или самостоятельных заданий.
Метод «бриллиантовой бумаги»
На уроках математики школьникам часто выдают листы с набором практически одинаковых примеров, которые надо решить. Когда это происходит, они упускают возможность укрепить нейронные связи. Значительно полезнее выбрать три-четыре примера и решить их разными способами.
Один из способов развития многопланового подхода — использование «бриллиантовой бумаги». Идея состоит в том, чтобы сложить лист бумаги следующим образом.
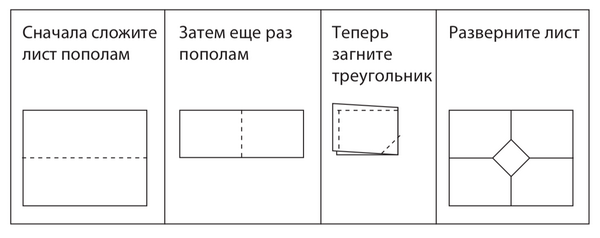
Сложите лист бумаги таким образом
Поместите пример в центр листа, а чистые четыре четверти используйте для демонстрации разных способов решения. Вот как можно использовать «бриллиантовый лист» для примера 50 ÷ 8.
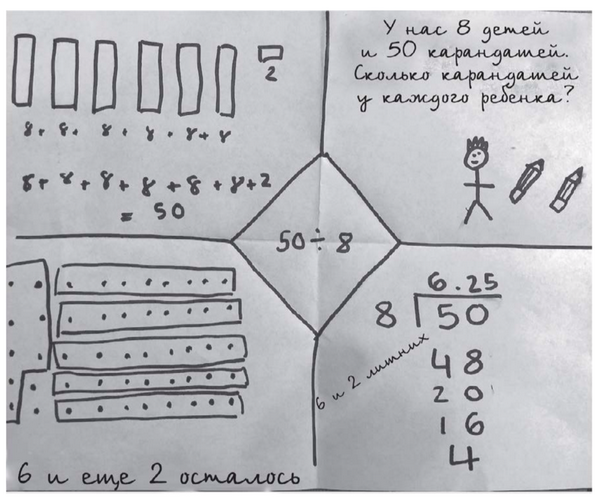
Методов решения задачи может быть гораздо больше
Когда ученик постигает предмет в разных форматах, у него возникают новые нейронные пути, которые позволяют разным, прежде изолированным участкам мозга взаимодействовать между собой, создавая тот тип связей, который исследователи обнаруживают в мозге новаторов.
Упражнение «Семь точек»
Покажите ребенку рисунок с семи точками на очень короткое время и попросите ответить, сколько точек нарисовано, причем считать надо не по одной, а попробовать мыслить блоками. Вот этот рисунок.

Мыслить блоками — это означает способы группировки. На рисунке ниже вы увидите примеры.
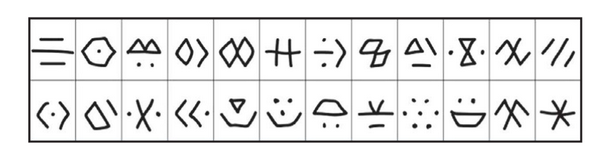
Визуальное представление семи точек 24 разными способами
Это упражнение здорово иллюстрирует креативность математики — даже на уровне семи точек! И это упражнение одновременно развивает участок мозга, отвечающий за интуитивное чувство числа. Оно позволяет оценить размер группы однотипных предметов на глаз. Как выяснилось, по степени развитости интуитивного чувства числа можно точно спрогнозировать успеваемость по математике.
Упражнение «Четыре четверки»
Предложите ученику представить каждое число от 1 до 20, используя четыре четверки и любые операции. Смысл в том, чтобы придумать как можно более разнообразные варианты. Используйте сложение, вычитание, деление, дроби и так далее.
Дайте ответ
Еще одно интересное задание на креативность и гибкость мышления. Напишите ответ и спросите, сколькими способами мы можем его получить? Например, напишите цифру 17. Самый простой вариант — это «1 + 16». Можно предложить множество разных вариантов, при этом от души повеселиться.
Метод Гаусса
Исключительно эффективный математический навык — упрощать. Когда мы ищем решение сложной задачи, используя меньшие числа, то присущие ей закономерности часто становятся более понятными и осязаемыми. К примеру, рассмотрим изящное доказательство, известное как доказательство Гаусса.
Не известно, насколько эта история правдива, но приведем ее здесь, чтобы освежить в памяти, что такое метод Гаусса. Когда Карл Гаусс учился в начальной школе, преподаватель понял, что ему необходимо давать сложные задачи, и, чтобы занять его на долгое время, попросил сосчитать сумму чисел от 1 до 100. Но маленький Карл заметил одну любопытную закономерность и понял, что необязательно складывать все числа, ведь сумма пар чисел, равноудаленных от концов, одинакова: 1+100=101, 2+99=101, 3+98=101… 50+51 = 101 и так далее, и что таких пар ровно 50. Результат был получен мгновенно: 50 × 101 = 5050.
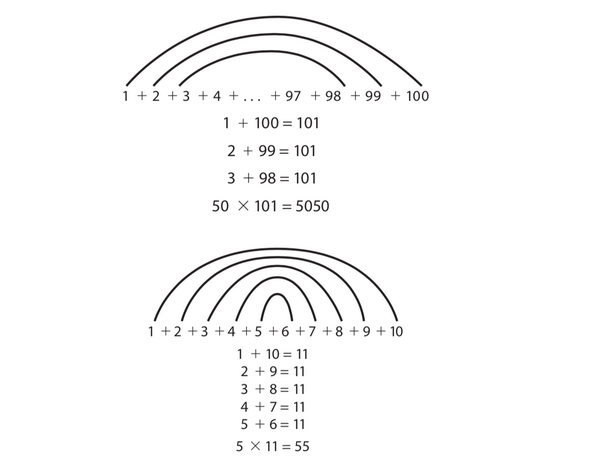
Способ вычисления суммы целых чисел от 1 до 100, примененный Карлом Гауссом, и пример с вычислением суммы целых чисел от 1 до 10
Если вам захочется испытать ребенка (и себя) и не упустить возможность для развития мозга, рекомендуем подумать, как метод Гаусса работает на примере последовательности, состоящей из нечетного количества целых чисел.
В жизни крайне важно научиться играть с числами и рассматривать математику как предмет, к которому стоит относиться открыто и многопланово. В книге «Безграничный разум» вы найдете больше способов, как подружиться с математикой.
Обложка поста: unsplash.com







