«Алиса в стране чудес» — одна из самых удивительных и фантастических сказок. Однако ученые готовы предположить, что и падение в кроличью нору, и уменьшение Алисы, и безумное чаепитие вполне реальны. И даже объяснить всё это с точки зрения науки.
В книге «Алиса в стране наук» биолог, математик и физик рассказывают, как приключения, описанные Льюисом Кэрроллом, могли случиться на самом деле.
Падение в кроличью нору с точки зрения физики
А она все падала и падала. Неужели этому не будет конца?
— Интересно, сколько миль я уже пролетела? — сказала Алиса вслух. — Я, верно, приближаюсь к центру Земли. Дайте-ка вспомнить… Это, кажется, около четырех тысяч миль вниз.
Л. Кэрролл, «Приключения Алисы в Стране чудес»

Полет сквозь Землю. Иллюстрация из книги
Погнавшись за Белым Кроликом, Алиса провалилась в колодец и полетела вниз. Но почему именно вниз? Что за сила влекла ее? Сила собственной тяжести — это раз. Но кроме Алисы в этой истории задействовано куда более массивное тело — наша планета.
Великий ученый Исаак Ньютон понял, что все тела притягиваются друг к другу. Именно эта сила удерживает Луну на орбите нашей планеты и не дает ей улететь в открытый космос. Эта же сила заставляет яблоко падать на землю, а Алису лететь вниз в колодце.
Ньютон назвал эту силу термином «тяготение», или «гравитация» — от латинского слова gravis, что значит «тяжелый». Но какова ее природа, понять не смог.
Только в начале ХХ века Альберт Эйнштейн догадался, откуда она берется. Согласно его общей теории относительности, всякое тело искривляет пространство вокруг себя, и именно это искривление мы ощущаем как земное притяжение.
При этом сама Алиса, падая, не ощущает притяжения, и если она закроет глаза, то может подумать, что парит в невесомости.
Уменьшение Алисы с точки зрения биологии
— Какое странное ощущение! — воскликнула Алиса. — Я, верно, складываюсь, как подзорная труба.
И не ошиблась — в ней сейчас было всего десять дюймов росту.
Л. Кэрролл, «Приключения Алисы в Стране чудес»

Уменьшение Алисы. Иллюстрация из книги
Алиса — человек, следовательно, она млекопитающее. Млекопитающие теплокровны, а значит, температура их тела не зависит от температуры окружающей среды. До каких размеров Алиса могла бы уменьшиться, сохраняя теплокровность?
Самые маленькие млекопитающие на Земле — карликовые многозубки. Они достигают 3–4,5 см в длину и весят около 1,7–2 граммов. Такое маленькое животное теряет тепло очень быстро. Чтобы компенсировать потери энергии, оно вынуждено съедать за сутки пищи вдвое-втрое больше собственного веса.
Фактически многозубки почти всю жизнь проводят в поисках еды. Для некоторых из них даже двухчасовая голодовка смертельна. Кроме того, для получения энергии необходимо очень много кислорода, переносимого кровью. Поэтому сердце этих животных сокращается 1300–1500 раз в минуту!
Множество ничего с точки зрения математики
— Они рисовали мышеловки, месяц, математику, множество… Ты когда-нибудь видела, как рисуют множество?
— Множество чего? — спросила Алиса.
— Ничего, — отвечала Соня. — Просто множество!
Л. Кэрролл, «Приключения Алисы в Стране чудес»
В математике множество — это любая совокупность объектов, ни один из которых не повторяется. Какие именно объекты входят в множество, не важно: это могут быть буквы, цифры, слова…
Знаменитый математик Леонард Эйлер еще в XVIII веке предложил рисовать множества с помощью кругов. Этот способ стал популярным после выхода книги Джона Венна «Символическая логика», потому и называется «диаграмма Венна».
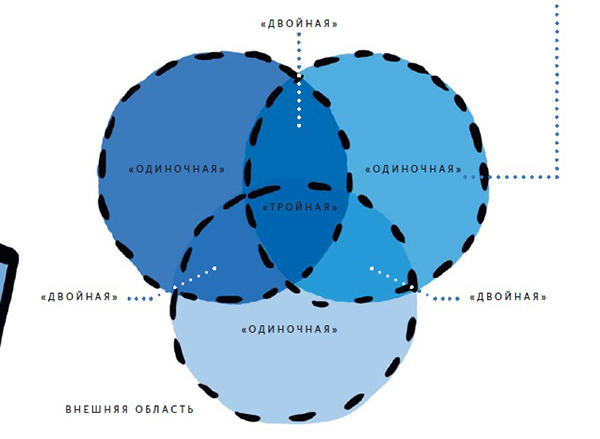
Как устроены эти диаграммы? Рассмотрим пример для трех множеств. Каждое из множеств изображается в виде круга, в котором находятся элементы этого множества. Те элементы, которые входят одновременно в два множества, размещаются в общей части двух кругов (это пересечение двух множеств).
 ,
,
Диаграмма Венна. Иллюстрация из книги
А есть и элементы, которые входят во все три множества, — они находятся в части, общей для всех трех кругов.
Четыре или пять множеств изобразить кругами на диаграмме Венна уже не получится, однако вместо кругов в этом случае можно использовать эллипсы. Попробуйте нарисовать такую диаграмму.
По материалам книги «Алиса в стране наук».







