В книге «Капуста, неверные мужья и зебра» содержится 125 головоломок, созданных за прошедших два тысячелетия, вместе с историями об их происхождении и влиянии. Мы выбрали 10 из них, чтобы вы смогли проверить себя. Подростки тоже могут справиться, если хорошенько подумают. Эти загадки на мышление.
Правила: пользоваться калькуляторами не разрешается.
Задачи:
1. На рисунке показан вид одного и того же куба с трех разных сторон. Какая буква находится на грани, противоположной грани с буквой U?
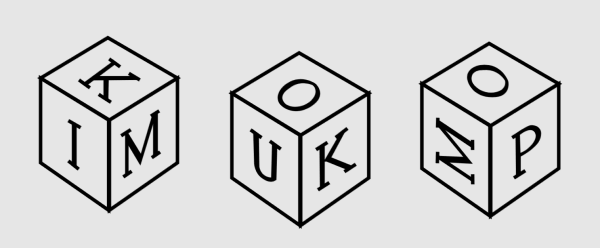
Варианты ответов: а) I; б) P; в) K; г) M; д) O.

Капуста, неверные мужья и зебра
2. Длина носа Пиноккио 5 сантиметров. Каждый раз, когда он говорит неправду, длина его носа удваивается. Когда Пиноккио соврет девять раз, длина его носа примерно будет равна длине:
Варианты ответов: а) костяшки домино; б) теннисной ракетки; в) бильярдного стола; г) теннисного корта; д) футбольного поля.
3. В слове thirty (30) 6 букв, а 30 = 6 × 5. Аналогично в слове fourty (40) 5 букв, а 40 = 5 × 8. Какие из следующих слов обозначают числа, не кратные количеству букв в этом слове?
Варианты ответов: а) six (6); б) twelve (12); в) eighteen (18); г) seventy (70); д) ninety (90).
4. Эми, Бен и Крис стоят в ряд. Если Эми стоит слева от Бена, а Крис справа от Эми, то какое из следующих утверждений верно?
Варианты ответов: а) Бен — крайний слева; б) Крис — крайний справа; в) Эми стоит посредине; г) Эми — крайняя слева; д) ни одно из предыдущих утверждений не верно.
5. Какие из изображений можно нарисовать, не отрывая карандаша от бумаги и не проводя им по линии второй раз?
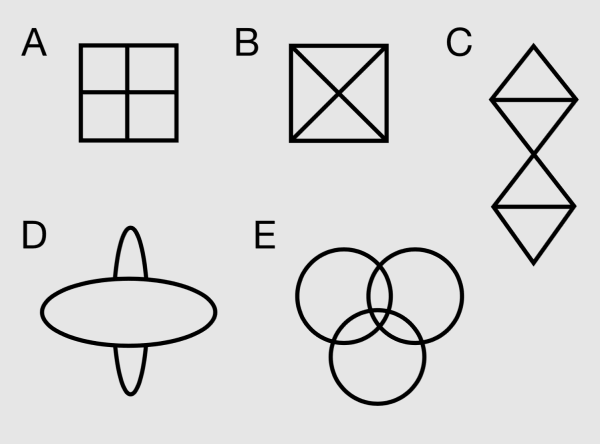
6. Чему равен остаток при делении числа 354 972 на 7?
Варианты ответов: а) 1; б) 2; в) 3; г) 4; д) 5.
7. У каждого ребенка в данной семье есть хотя бы один брат и хотя бы одна сестра. Какое минимальное количество детей в этой семье?
Варианты ответов: а) 2; б) 3; в) 4; г) 5; д) 6.
8. Сколько раз цифра 8 встречается в произведении 987 654 321 × 9?
Варианты ответов: а) 1; б) 2; в) 3; г) 4; д) 9.
9. В каждом прямоугольнике частично заполненной пирамиды необходимо записать число, равное сумме двух чисел в прямоугольниках, расположенных непосредственно под ним. Какое число находится на месте х?
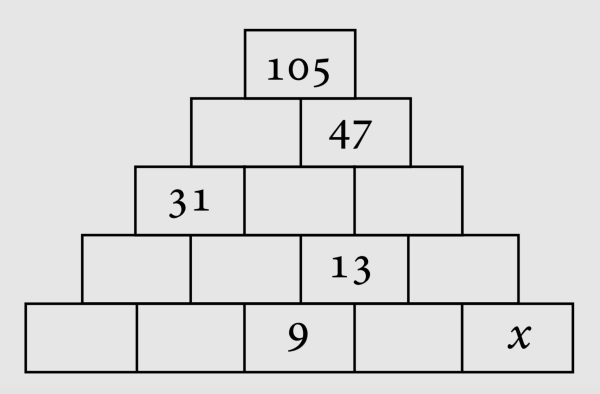
Варианты ответов: а) 3; б) 4; в) 5; г) 7; д) 12.
10. Сколько разных цифр присутствует в периодической десятичной дроби, соответствующей дроби 20/11
Варианты ответов: а) 2; б) 3; в) 4; г) 5; д) 6.
Ответы:
1. г) М.
На рисунке видно, что на кубе изображено шесть букв: I, K, M, O, U и P. Поскольку у куба шесть граней, на нем могут быть написаны только эти буквы. На первой картинке грани с буквами I и M имеют общее ребро с гранью буквы K. На второй — общее ребро с гранью буквы K у O и U. Только у четырех граней может быть общее ребро с гранью буквы K. Если расположить куб так, чтобы грань с буквой K была сверху (как на первой картинке), то грань с буквой I будет смежной грани с буквой M по часовой стрелке. На основании второй картинки мы можем сделать вывод, что, когда грань с буквой K находится сверху, грань с буквой O смежна грани с буквой U по направлению движения часовой стрелки, а значит, грани куба расположены по часовой стрелке в следующем порядке: M-I-U-O. Таким образом, на грани, противоположной грани с буквой U, находится буква M.

Чек-лист с простыми и доступными упражнениями, цель которых — очистить и перенастроить мозг→
2. г) теннисного корта.
После того как Пиноккио солжет девять раз, длина его носа составит 29 × 5 см = 512 × 5 см = 25,6 м, что примерно равно длине теннисного корта, которая равна 23,8 метра. Однако, согласно отчету Центра междисциплинарных наук при Университете Лестера, эта длина намного меньше возможной максимальной длины носа Пиноккио. Расчеты специалистов центра показывают, что если деревянная голова Пиноккио весит 4,18 килограмма, а нос — 6 граммов, первоначальная длина которого составляет один дюйм (2,54 см), то нос сломается только после 13 случаев вранья, когда он вырастет до 208 метров.
3. в) eighteen (18).
В слове eighteen (18) восемь букв, а число 18 не кратно 8.
4. г) Эми — крайняя слева.
Эми находится по левую сторону и от Бена, и от Криса. Следовательно, эти трое стоят в таком порядке: Эми, Бен, Крис или Эми, Крис, Бен. Это все, что нам известно, поэтому утверждение «г» однозначно верно. Ни одно из оставшихся утверждений не должно быть истинным, хотя утверждение «б» может быть истинным.
5. E.
Эту задачу можно решить методом проб и ошибок. Можно также доказать следующее правило: чтобы нарисовать изображение, не отрывая карандаша от бумаги и не проводя карандашом по линии повторно, оно должно содержать не более двух точек, в которых сходится нечетное количество линий. Этому условию удовлетворяет только ответ E, поскольку на изображении вообще нет точек, в которых сходится нечетное количество линий, тогда как на других рисунках таких точек больше двух*.
* Назовем точку, в которой сходится нечетное количество линий, нечетной, а ту, в которой сходится четное количество линий, четной. Вот полное правило, при условии соблюдения которого можно нарисовать изображение, не отрывая карандаша от бумаги:
-
- если в изображении нет нечетных точек, то его можно нарисовать одним движением, не отрывая карандаша от бумаги, начиная с любого места;
- если в изображении две нечетные точки, то его можно нарисовать непрерывным движением, причем начинать нужно с одной нечетной точки, а заканчивать в другой;
- если в изображении более двух нечетных точек, то его нельзя начертить одним движением карандаша.
Эти правила — парафраз теорем из теории графов. Прим. ред.
6. б) 2.
Надеюсь, вы знаете хотя бы таблицу умножения на семь! В таком случае для вас не станет неожиданностью тот факт, что 35 делится на 7, а значит, и 350 000 делится на 7. На 7 делится также 49, и 4900. Поскольку 354 972 = 350 000 + 4900 + + 72, остается только найти остаток от деления 72 на 7. Так как 7 × 10 = 70, остаток равен 2.
7. в) 4.
В семье должно быть по меньшей мере два мальчика, поскольку если бы мальчик был только один, у него не было бы брата, что противоречит условиям задачи. Аналогично, в семье должно быть по меньшей мере две девочки, а значит, в семье минимум четверо детей.
8. д) 9.
Просто выполните это забавное умножение на любом клочке бумаги — и задача решена.
98765432 1 × 9 = 8888888889
9. а) 3.
Надеюсь, на вашем листе бумаги еще осталось место. Впишите в пустые клетки пирамиды (начиная сверху и слева направо) буквы p, q, r; в правую крайнюю клетку в четвертом ряду s и в пятом ряду между клетками с числом 9 и буквой х — t. Вот необходимые вычисления:
p = 105 — 47 = 58;
q = p — 31 = 58 — 31 = 27; r = 47 — q = 47 — 27 = 20; s = r — 13 = 20 — 13 = 7;
t = 13 — 9 = 4;
х = s — t = 7 — 4 = 3.
10. а) 2.
Было бы неучтиво не включить задачу на деление в столбик, в результате чего получим 20/11 = 1,818181… поэтому десятичная дробь содержит только две разные цифры.
Из книги «Капуста, неверные мужья и зебра»
Обложка поста: unsplash.com







